|
|
¡¡ |
¡¡
Motor Control and Movement Disorder in The Basal Ganglia
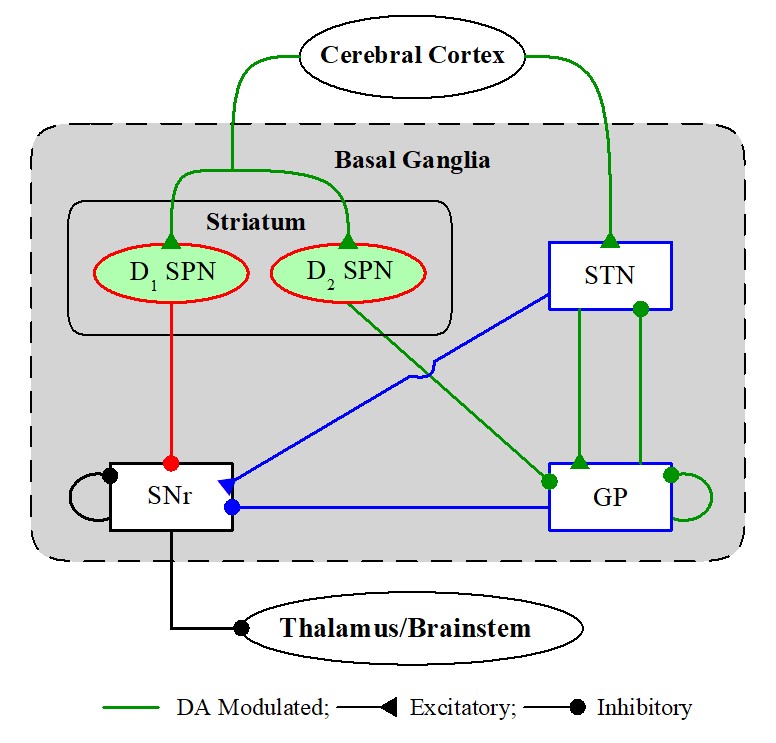
(1) Population Oscillatory and Individual Firing Behaviors in A Spiking Neural Network of The Basal Ganglia
The basal ganglia (BG) (called the dark basement of the brain) are group of subcortical deep-
lying nuclei located at the base of the Forebrain. The striatum (primary input to the BG) is the
largest component with stripped appearance, consisting of primarily medium-sized spiny
projection neurons (SPNs) with D1/D2 receptors to the dopamine (DA); these SPNs receive
cortical inputs. Subthalamic Nucleus (STN) is another input nucleus receiving the cortical
input and it is the only excitatory nucleus in the BG. Substantia Nigra pars Reticulata (SNr)
is the output nucleus of the BG in the rat brain. The Globus Pallidus (GP) in the rat is the
intermediate control nucleus. The main functions of the BG are control of voluntary motor
movement, procedural learning (i.e., acquisition of motor skills and habits, a certain types of
cognitive skills), cognition and emotion. There are two pathways in the BG; direct pathway
(D1 SPN ¡æ SNr) facilitating movement and indirect pathway (D2 SPN ¡æ GP ¡æ STN ¡æ SNr)
suppressing movement. Diverse functions of the BG may be done via balance between
the direct and indirect pathways. The antagonistic functions of the direct and indirect pathways
are modulated by the DA. DA release has opposite effects on the direct and indirect pathways;
DA enhances the direct pathway, while it suppresses the indirect pathway (via releasing the
brake). As a result of imbalance between the direct and indirect pathway, movement disorder
such as Parkinson's disease occurs due to DA depletion. Also, in the neurodegerative disease
(e.g., Alzheimer's disease), reduction in healthy synapses and synaptic strength occurs. Hence,
we investigate population and individual firing behaviors in the default, the healthy and the
pathological PD states in the BG by changing the DA level and the synaptic parameters (e.g.,
maximum conductance, connection probability, cell ablation). Particularly, we are interested
in synchronization in the PD state; how to change depending on the above change in the
parameters. Effect of cell ablation (STN or SNr) (similar to DBS) on the synchronization in the
PD state is also studied. More fundamentally, we also try to clearly understand the roles of the
direct and indirect pathways and their balance; particularly, the role of indirect pathway is
somewhat unclear.
¡¡
Memory Formation, Storage, and Retrieval in The Hippocampus

(1) Pattern Separation and Sparsely Synchronized Rhythms in The Hippocampal Dentate Gyrus
The hippocampus, consisting of the dentate gyrus (DG) and the areas CA3 and CA1, plays important roles in memory formation, storage, and retrieval
(e.g., episodic and spatial memory). The DG is the gateway to the hippocampus, and its excitatory granule cells (GCs) receive excitatory inputs
from the entorhinal cortex (EC) via the perforant paths (PPs). As a pre-processor for the CA3, the principal GCs perform pattern separation on the
input patterns from the EC by sparsifying and orthogonalizing them, and send the pattern-separated outputs to the pyramidal cells in the CA3 through
the mossy fibers (MFs). Then, the sparse, but strong MFs play a role of ``teaching inputs,'' causing synaptic plasticity between the pyramidal cells
in the CA3. Thus, a new pattern may be stored in modified synapses. In this way, pattern separation in the DG may facilitate pattern storage in the CA3.
In the DG, firing activities of the GCs become sparse via the winner-take-all competition; only strongly active GCs may survive under strong feedback
from the inhibitory basket cells. We also note that, during pattern separation sparsely synchronized rhythm (SSR) of the GCs appear. Population and
individual firing behaviors of the SSR is strongly correlated with pattern separation. The larger population synchronization degree of the SSR is,
the better the pattern separation efficacy becomes.
[1] S.-Y. Kim and W. Lim, "Dynamical origin for winner-take-all competition in a biological network of the hippocampal dentate gyrus," Physical Review E 105, 014418 (2022).
[2] S.-Y. Kim and W. Lim, "Population and individual firing behaviors in sparsely synchronized rhythms in the hippocampal dentate gyrus," Cognitive Neurodynamics 16, 643-665 (2022).
[3] S.-Y. Kim and W. Lim, "Disynaptic effect of hilar cells on pattern separation in a spiking neural network of hippocampal dentate gyrus," Cognitive Neurodynamics 16, 1427-1447 (2022).
(2) Effect of Adult Neurogenesis on Pattern Separation and Sparsely Synchronized Rhythms in The Dentate Gyrus
One of the most distinctive characteristics of the dentate gyrus (DG) which is the gateway to the hippocampus is occurrence of adult neurogenesis which results
in the generation of new granule cells (GCs) during adulthood. The new GCs born in the subgranular zone migrate into the granular layer of the DG. The whole population
of GCs is thus composed of mature GCs (mGCs) born during the development and adult-born immature GCs (imGCs). In contrast to the mGCs, the young adult-born imGCs are
known to have marked properties such as high excitability, weak inhibition, and low excitatory innervation. Due to their high excitability, the imGCs have strong
correlation between them, and they exhibit pattern integration (making association between patterns). Thus, the whole population of GCs becomes a heterogeneous one,
composed of a (major) subpopulation of mGCs (i.e., pattern separators) and a (minor) subpopulation of imGCs (i.e., pattern integrators). Due to presence of the imGCs,
pattern separation efficacy and sparsely synchronized rhythms in the whole heterogeneous population become deteriorated. However, memory resolution might be increased
via mixed encoding (through pattern separation (mGCs) and pattern integration (imGCs)), which could reduce memory interference.
[1] S.-Y. Kim and W. Lim, "Effect of adult-born immature granule cells on pattern separation in the hippocampal dentate gyrus," BioRxiv, DOI: 10.1101/2023.01.12.523852.
¡¡
Effect of Diverse Recoding of Granule Cells on Optokinetic Response and Delay Eyeblink Conditioning in A Cerebellar Ring Network with Synaptic Plasticity
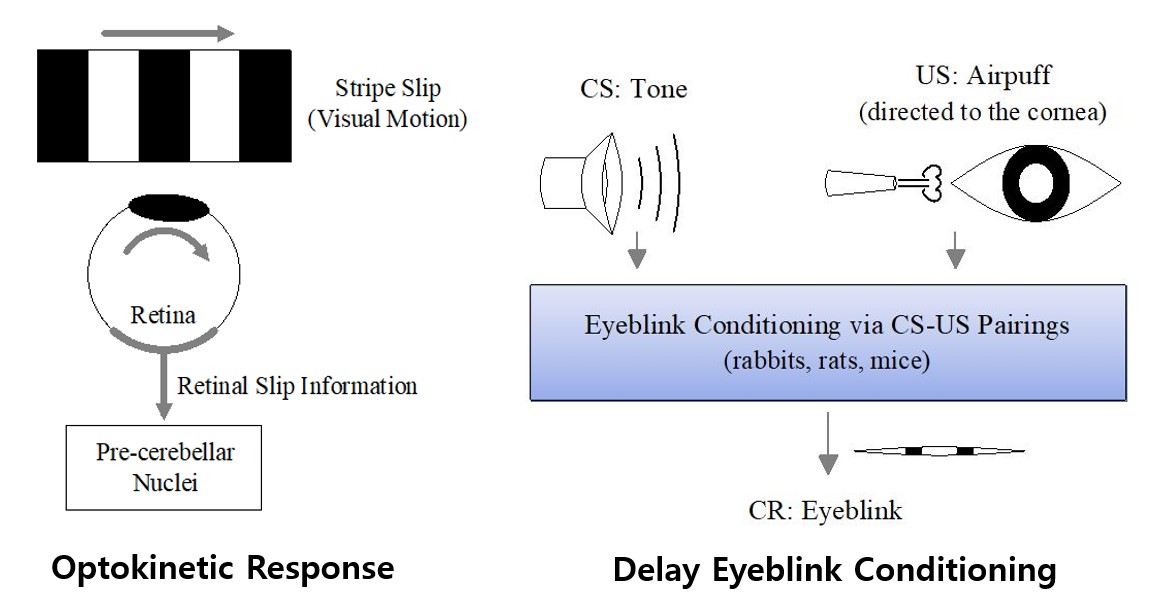
We develop a cerebellar ring network, and investigate the effect of diverse recoding of granule (GR) cells on optokinetic response (OKR associated with spatial motor control) and delay Pavlovian eyeblink conditioning
(EBC related to temporal motor control) by varying the connection probability pc from Golgi to GR cells. For an optimal value of pc, individual GR cells exhibit diverse spiking patterns. In the case of OKR, they are
in-phase, anti-phase, or complex out-of-phase with respect to their population averaged firing activity. In the case of EBC, individual granule cells show various
well- and ill-matched firing patterns relative to the unconditioned stimulus. Then, these diversely-recoded signals are fed into the Purkinje cells (PCs) through parallel-fibers (PFs),
and the instructor climbing-fiber (CF) signals from the inferior olive depress them effectively.
For the OKR, synaptic weights at in-phase PF-Purkinje cell (PC) synapses of active GR cells are strongly depressed via strong long-term depression (LTD), while those at
anti-phase and complex out-of-phase PF-PC synapses are weakly depressed through weak LTD. Similar synaptic plasticity also occurs for the EBC.
In the case of well-matched PF-PC synapses, their synaptic weights are strongly depressed through strong long-term depression (LTD). On the other hand, practically no LTD occurs
for the ill-matched PF-PC synapses. This kind of effective depression (i.e., strong/weak LTD) at the PF-PC synapses causes a big modulation in firings of PCs.
Then, PCs exert effective inhibitory coordination on the vestibular nucleus (VN) neuron (which evokes OKR) doe the OKR and
cerebellar nucleus neuron [which elicits conditioned response (CR)] for the eyeblink conditioning.
In the case of OKR, for the firing of the VN neuron, the learning gain degree Lg, corresponding to the modulation gain ratio, increases with increasing the learning cycle, and it
saturates. In the case of EBC, when the learning trial passes a threshold, acquisition of CR begins. In this case, the timing degree Td of CR becomes good due to
presence of the ill-matched firing group which plays a role of protection barrier for the timing. With further increase in the trial, strength S of CR (corresponding to the amplitude of eyelid closure)
increases due to strong LTD in the well-matched firing group, while its timing degree Td decreases. In this way, the well- and the ill-matched firing groups play their own roles
for the strength and the
timing of CR, respectively. Thus, with increasing the learning trial, the (overall) learning efficiency Le (taking into consideration both timing and strength of CR) for the CR is increased, and
eventually it becomes saturated. By changing pc from its optimal value, we also investigate the effect of diverse recoding on the OKR and the EBC. It is thus found that the more diverse
in recoding of GR cells, the more effective in motor learning for the OKR and the Pavlovian EBC.
[1] S.-Y. Kim and W. Lim, "Effect of diverse recoding of granule cells on optokinetic response in a cerebellar ring network with synaptic plasticity," Neural Networks 134, 173-204 (2021).
[2] S.-Y. Kim and W. Lim, "Influence of various temporal recoding on Pavlovian eyeblink conditioning in the cerebellum," Cognitive Neurodynamics 15, 1067-1099 (2021).
¡¡
Effect of Synaptic Plasticity on Brain Rhythms, Associated with Diverse Brain Functions and Diseases, in Complex Biological Neural Networks
(1) Effect of Intrapopulation Spike-Timing-Dependent Plasticity on Synchronized Rhythms in Complex Neural Networks
We consider a complex neural network consisting of excitatory (E) or inhibitory (I) spiking or bursting neurons.
This neuronal network has adaptive dynamic E to E or I to I intrapopulation synaptic strengths governed by the spike-timing-dependent plasticity (STDP).
In previous works without STDP, synchronized population rhythm was found to occur in a range of intermediate noise intensities.
We investigate the effect of additive STDP on the synchronized rhythm by varying the noise intensity. Occurrence of a "Matthew" effect
in synaptic plasticity is found due to a positive feedback process. As a result, good synchronization gets better via long-term potentiation (LTP)
of synaptic strengths, while bad synchronization gets worse via long-term depression (LTD). Furthermore, emergences of long-term potentiation
and long-term depression of synaptic strengths are intensively investigated via microscopic studies based on the distributions of time delays between the pre- and the post-synaptic spike times.
[1] S.-Y. Kim and W. Lim, "Stochastic spike synchronization in a small-world neural network with spike-timing-dependent plasticity," Neural Networks 97, 92-106 (2018).
[2] S.-Y. Kim and W. Lim, "Effect of spike-timing-dependent plasticity on stochastic burst synchronization in a scale-free neuronal network," Cognitive Neurodynamics 12, 315-342 (2018).
[3] S.-Y. Kim and W. Lim, "Effect of inhibitory spike-timing-dependent plasticity on fast sparsely synchronized rhythms in a small-world neuronal network," Neural Networks 106, 50-66 (2018).
[4] S.-Y. Kim and W. Lim, "Burst synchronization in a scale-free neuronal network with inhibitory spike-timing-dependent plasticity," Cognitive Neurodynamics 13, 53-73 (2019).
(2) Effect of Interpopulation Spike-Timing-Dependent Plasticity on Synchronized Rhythms in Neuronal Networks with Inhibitory and Excitatory Populations
We consider a two-population network consisting of both inhibitory (I) interneurons and excitatory (E) pyramidal cells. This I-E neuronal network has adaptive dynamic I to E and E to I interpopulation
synaptic strengths, governed by interpopulation spike-timing-dependent plasticity (STDP). In previous works without STDPs, fast sparsely synchronized rhythms, related to diverse cognitive functions,
were found to appear in a range of noise intensity D for static synaptic strengths. Here, by varying D, we investigate the effect of interpopulation STDPs on fast sparsely synchronized rhythms
that emerge in both the I- and the E-populations. Depending on values of D, long-term potentiation (LTP) and long-term depression (LTD) for population-averaged values of saturated interpopulation synaptic strengths
are found to occur. Then, the degree of fast sparse synchronization varies due to effects of LTP and LTD. In a broad region of intermediate D, the degree of good synchronization (with higher synchronization degree)
becomes decreased, while in a region of large D, the degree of bad synchronization (with lower synchronization degree) gets increased. Consequently, in each I- or E-population, the synchronization degree becomes
nearly the same in a wide range of D (including both the intermediate and the large D regions). This kind of "equalization effect" is found to occur via cooperative interplay between the average
occupation and pacing degrees of spikes (i.e., the average fraction of firing neurons and the average degree of phase coherence between spikes in each synchronized stripe of spikes in the raster plot of spikes)
in fast sparsely synchronized rhythms. Finally, emergences of LTP and LTD of interpopulation synaptic strengths (leading to occurrence of equalization effect) are intensively investigated via a microscopic method
based on the distributions of time delays between the pre- and the post-synaptic spike times.
[1] S.-Y. Kim and W. Lim, "Effect of interpopulation spike-timing-dependent plasticity on synchronized rhythms in neuronal networks with inhibitory and excitatory populations," Cognitive Neurodynamics 14, 535-567 (2020).
¡¡
Sparsely
Synchronized Brain Rhythms in Complex Neural Networks
Sparsely-synchronized brain rhythms,
associated with diverse cognitive functions such as sensory perception, feature
integration, selective attention, and memory formation, have been observed in
electric recordings (e.g., EEG and local field potentials) of brain activity. At
the population level, cortical rhythms exhibit small-amplitude fast
oscillations, while at the cellular level individual neurons show stochastic
firings sparsely at a much lower rate than the population rate. To resolve the
apparent dichotomy between synchrony at the population level and stochasticity
at the cellular level, we study emergence of sparsely synchronized brain rhythms
in networks of Geiger-counter-like neurons exhibiting irregular discharges.
Previously, sparse synchronization was found to occur for cases of both global
coupling (i.e., regular all-to-all coupling) and random coupling. However, a
real neural network is known to be non-regular and non-random because it has
complex topology (e.g., small-worldness, scale-freeness, and modularity). Hence,
we investigate the effect of the network architecture on emergence of sparsely
synchronized rhythms in real complex networks such as the small-world, the
scale-free, the star-like, and the clustered networks.
(1) Sparsely Synchronized Brain Rhythm in A Small-World
Neural Network
Sparsely synchronized cortical
rhythms, associated with diverse cognitive functions, have been
observed in electric recordings of brain activity. At the population
level, cortical rhythms exhibit small-amplitude fast oscillations,
while at the cellular level, individual neurons show stochastic
firings sparsely at a much lower rate than the population rate. We
study the effect of network architecture on sparse synchronization
in an inhibitory population of Geiger-counter-like neurons showing
stochastic discharges. As an element of the network, we consider the
subthreshold Morris-Lecar neuron and the fast spiking Izhikevich
interneuron which fires as Geiger counters. When strong external
noise balances with strong synaptic inhibition, sparsely
synchronized rhythms are found to emerge. Previously, sparse
synchronization was found to occur for both cases of global coupling
(i.e., regular all-to-all coupling) and random coupling. However, a
real neural network is known to be neither regular, nor random.
Here, we consider sparse Watts-Strogatz small-world networks which
interpolates between the regular lattice and the random graph via
rewiring. We start from the regular lattice with only short-range
connections, and then investigate emergence of sparse
synchronization by increasing the rewiring probability p from
short-range to long-range connections. For p=0, the average synaptic
path length between pairs of neurons becomes long, and hence there
exists only an unsynchronized population state because the global
efficiency of information transfer is low. However, as p is
increased, long-range connections begin to appear, and global
effective communication between distant neurons may be available via
shorter synaptic paths. Consequently, as p passes a threshold pth,
sparsely synchronized population rhythms emerge. However, with
increasing p longer axon wirings become expensive because of their
material and energy costs. At an optimal value p*DE
of the rewiring probability, the ratio of the synchrony degree to
the wiring cost is found to become maximal. In this way, an optimal
sparse synchronization is found to occur at a minimal wiring cost in
an economic small-world network through trade-off between synchrony
and wiring cost.
[1] S.-Y. Kim and W. Lim,
"Sparsely-synchronized brain rhythm in a small-world neural network"
J. Korean Phys. Soc. 63, 104-113 (2013).
[2]
S.-Y. Kim and W. Lim,
"Effect of small-world connectivity on fast sparsely
synchronized cortical rhythms,"
Physica A 421, 109-123 (2015).
(2) Sparsely Synchronized Brain Rhythm in A Scale-Free
Neural Network
We consider a directed version of
the Barabasi-Albert scale-free network model with symmetric
preferential attachment with the same in- and out-degrees and study
the emergence of sparsely synchronized rhythms for a fixed
attachment degree in an inhibitory population of fast-spiking
Izhikevich interneurons. Fast sparsely synchronized rhythms with
stochastic and intermittent neuronal discharges are found to appear
for large values of J (synaptic inhibition strength) and D (noise
intensity). For an intensive study we fix J at a sufficiently large
value and investigate the population states by increasing D. For
small D, full synchronization with the same population-rhythm
frequency fP and mean firing rate (MFR) fi of
individual neurons occurs, while for large D partial synchronization
with fP > <fi> (<fi>:
ensemble-averaged MFR) appears due to intermittent discharge of
individual neurons; in particular, the case of fP > 4<fi>
is referred to as sparse synchronization. For the case of partial
and sparse synchronization, MFRs of individual neurons vary
depending on their degrees. As D passes a critical value D*
(which is determined by employing an order parameter), a transition
to unsynchronization occurs due to the destructive role of noise to
spoil the pacing between sparse spikes. For D<D*,
population synchronization emerges in the whole population because
the spatial correlation length between the neuronal pairs covers the
whole system. Furthermore, the degree of population synchronization
is also measured in terms of two types of realistic
statistical-mechanical measures. Only for the partial and sparse
synchronization do contributions of individual neuronal dynamics to
population synchronization change depending on their degrees, unlike
in the case of full synchronization. Consequently, dynamics of
individual neurons reveal the inhomogeneous network structure for
the case of partial and sparse synchronization, which is in contrast
to the case of statistically homogeneous random graphs and
small-world networks. Finally, we investigate the effect of network
architecture on sparse synchronization for fixed values of J and D
in the following three cases: (1) variation in the degree of
symmetric attachment, (2) asymmetric preferential attachment of new
nodes with different in- and out-degrees, and (3) preferential
attachment between pre-existing nodes (without addition of new
nodes). In these three cases, both relation between network topology
(e.g., average path length and betweenness centralization) and
sparse synchronization and contributions of individual dynamics to
the sparse synchronization are discussed.
[1] S.-Y. Kim and W. Lim, "Fast sparsely
synchronized brain rhythms in a scale-free neural network," Phys.
Rev. E 92, 022717 (2015).
(3) Sparsely Synchronized Brain Rhythm in Clustered
Small-World Neural Networks
We consider a clustered network
with small-world sub-networks of inhibitory fast spiking
interneurons, and investigate the effect of inter-modular connection
on emergence of fast sparsely synchronized rhythms by varying both
the inter-modular coupling strength Jinter and the
average number of inter-modular links per interneuron M(inter)syn.
In contrast to the case of non-clustered networks, two kinds of
sparsely synchronized states such as modular and global
synchronization are found. For the case of modular sparse
synchronization, the population behavior reveals the modular
structure, because the intra-modular dynamics of sub-networks make
some mismatching. On the other hand, in the case of global sparse
synchronization, the population behavior is globally identical,
independently of the cluster structure, because the intra-modular
dynamics of sub-networks make perfect matching. We introduce a
realistic cross-correlation modularity measure, representing the
matching-degree between the instantaneous sub-population spike rates
of the sub-networks, and examine whether the sparse synchronization
is global or modular. Depending on its magnitude, the inter-modular
coupling strength Jinter seems to play ¡°dual¡± roles for
the pacing between spikes in each sub-network. For large Jinter,
due to strong inhibition it plays a destructive role to ¡°spoil¡± the
pacing between spikes, while for small Jinter it plays a
constructive role to ¡°favor¡± the pacing between spikes. Through
competition between the constructive and the destructive roles of Jinter,
there exists an intermediate optimal Jinter at which the
pacing degree between spikes becomes maximal. In contrast, the
average number of inter-modular links per interneuron M(inter)syn
seems to play a role just to favor the pacing between spikes. With
increasing M(inter)syn, the pacing degree
between spikes increases monotonically thanks to the increase in the
degree of effectiveness of global communication between spikes.
Furthermore, we employ the realistic sub- and whole-population order
parameters, based on the instantaneous sub- and whole-population
spike rates, to determine the threshold values for the
synchronization-unsynchronization transition in the sub- and
whole-populations, and the degrees of global and modular sparse
synchronization are also measured in terms of the realistic sub- and
whole-population statistical-mechanical spiking measures defined by
considering both the occupation and the pacing degrees of spikes. It
is expected that our results could have implications for the role of
the brain plasticity in some functional behaviors associated with
population synchronization.
[1] S.-Y. Kim and W. Lim, "Effect of inter-modular
connection on fast sparse synchronization in clustered small-world neural
networks," Phys. Rev. E 92, 052716 (2015).
Burst Synchronization in Complex Neural Systems
We are concerned about
population synchronization of bursting neurons. Bursting occurs when
neuronal activity alternates, on a slow timescale, between a silent
phase and an active (bursting) phase of fast repetitive spikings. This
type of bursting activity occurs due to the interplay of the fast ionic
currents leading to spiking activity and the slower currents modulating
the spiking activity. Hence, the dynamics of bursting neurons have two
timescales: slow bursting timescale and fast spiking timescale. These
bursting neurons exhibit two different patterns of synchronization due
to the slow and the fast timescales of bursting activity. Burst
synchronization (synchrony on the slow bursting timescale) refers to a
temporal coherence between the active phase (bursting) onset or offset
times of bursting neurons, while spike synchronization (synchrony on the
fast spike timescale) characterizes a temporal coherence between
intraburst spikes fired by bursting neurons in their respective active
phases. We study burst and spike synchronization of bursting neurons,
associated with neural information processes in health and disease, in
complex networks such as small-world, scale-free, and clustered
networks.
(1)
Stochastic Bursting Synchronization in A Population of Subthreshold
Izhikevich Neurons
We
are interested in neural bursting activity (alternating between a
silent phase and an active phase of repetitive spiking). Cortical
intrinsically bursting neurons, thalamocortical relay neurons,
thalamic reticular neurons, and hippocampal pyramidal neurons are
representative examples of bursting neurons. We investigate coherent
population dynamics in these bursting neurons by varying the noise
intensity D. Such coherence is well visualized in the raster plot of
neural spikings. For a coherent state, burst bands, composed of
stripes of spikes, constitute the raster plot. For this case, burst
synchronization refers to a temporal relationship between active
phase onset or offset times of bursting neurons, while spike
synchronization characterizes a temporal relationship between spikes
fired by different bursting neurons in their respective active
phases. For the coherent case, in addition to burst synchronization,
spike synchronization also occurs in each burst band. As a result of
this complete synchronization, the (ensemble-averaged) global
membrane potential VG exhibits a bursting activity like the local
membrane potential (i.e., fast spikes appear on a slow wave in VG).
However, as D is increased, loss of spike coherence first occurs in
each burst band due to smearing of stripes of spikes. With further
increase in D, overlapping between bands begins to occur, which
eventually leads to complete loss of burst synchronization. To
characterize these burst and spike coherence, we introduce a new
type of coherence measure quantifying the degree of coherence seen
in the raster plot of neural spiking, where the global potential is
used to give a reference phase for the burst onset times and the
spiking times in active phases.
[1]
S.-Y. Kim, Y. Kim, D.-G. Hong, J. Kim, and W. Lim, "Stochastic
bursting synchronization in a population of subthreshold Izhikevich
neurons", J. Korean Phys. Soc. 60, 1441-1447 (2012).
(2)
Coupling-Induced Population Synchronization in An Excitatory Population
of Subthreshold Izhikevich Neurons
We
consider an excitatory population of subthreshold Izhikevich neurons
which exhibit noise-induced firings. By varying the coupling
strength J, we investigate population synchronization between the
noise-induced firings which may be used for efficient cognitive
processing such as sensory perception, multisensory binding,
selective attention, and memory formation. As J is increased, rich
types of population synchronization (e.g., spike, burst, and fast
spike synchronization) are found to occur. Transitions between
population synchronization and incoherence are well described in
terms of an order parameter O. As a final step, the coupling induces
oscillator death (quenching of noise-induced spikings) because each
neuron is attracted to a noisy equilibrium state. The oscillator
death leads to a transition from firing to non-firing states at the
population level, which may be well described in terms of the
time-averaged population spike rate R. In addition to the
statistical- mechanical analysis using O and R, each population and
individual state are also characterized by using the techniques of
nonlinear dynamics such as the raster plot of neural spikes, the
time series of the membrane potential, and the phase portrait. We
note that population synchronization of noise-induced firings may
lead to emergence of synchronous brain rhythms in a noisy
environment, associated with diverse cognitive functions.
[1] S.-Y. Kim and W. Lim,
"Coupling-induced population synchronization in an excitatory
population of subthreshold Izhikevich neurons,"
Cognitive Neurodynamics 7, 495-503 (2013).
(3)
Noise-Induced Burst And Spike Synchronizations in An Inhibitory
Small-World Network of Subthreshold Bursting Neurons
We
are interested in noise-induced firings of subthreshold neurons
which may be used for encoding environmental stimuli. Noise-induced
population synchronization was previously studied only for the case
of global coupling, unlike the case of subthreshold spiking neurons.
Hence, we investigate the effect of complex network architecture on
noise-induced synchronization in an inhibitory population of
subthreshold bursting Hindmarsh–Rose neurons. For modeling complex
synaptic connectivity, we consider the Watts–Strogatz small-world
network which interpolates between regular lattice and random
network via rewiring, and investigate the effect of small-world
connectivity on emergence of noise-induced population
synchronization. Thus, noise-induced burst synchronization
(synchrony on the slow bursting time scale) and spike
synchronization (synchrony on the fast spike time scale) are found
to appear in a synchronized region of the J–D plane (J: synaptic
inhibition strength and D: noise intensity). As the rewiring
probability p is decreased from 1 (random network) to 0 (regular
lattice), the region of spike synchronization shrinks rapidly in the
J–D plane, while the region of the burst synchronization decreases
slowly. We separate the slow bursting and the fast spiking time
scales via frequency filtering, and characterize the noise-induced
burst and spike synchronizations by employing realistic order
parameters and statistical-mechanical measures introduced in our
recent work. Thus, the bursting and spiking thresholds for the burst
and spike synchronization transitions are determined in terms of the
bursting and spiking order parameters, respectively. Furthermore, we
also measure the degrees of burst and spike synchronizations in
terms of the statistical-mechanical bursting and spiking measures,
respectively.
[1]
S.-Y. Kim and W. Lim,
"Noise-induced burst and spike synchronizations in an inhibitory
small-world network of subthreshold bursting neurons," Cognitive
Neurodynamics 9, 179-200 (2015).
(4)
Effect of Network Architecture on Burst and Spike Synchronization in A
Scale-Free Network of Bursting Neurons
We
investigate the effect of network architecture on burst and spike
synchronization in a directed scale-free network (SFN) of bursting
neurons, evolved via two independent ¥á− and ¥â−processes. The
¥á−process corresponds to a directed version of the Barabasi-Albert
SFN model with growth and preferential attachment, while for the
¥â−process only preferential attachments between preexisting nodes
are made without addition of new nodes. We first consider the ¡°pure¡±
¥á−process of symmetric preferential attachment (with the same in-
and out-degrees), and study emergence of burst and spike
synchronization by varying the coupling strength J and the noise
intensity D for a fixed attachment degree. Characterizations of
burst and spike synchronization are also made by employing realistic
order parameters and statistical-mechanical measures. Next, we
choose appropriate values of J and D where only the burst
synchronization occurs, and investigate the effect of the scale-free
connectivity on the burst synchronization by varying (1) the
symmetric attachment degree and (2) the asymmetry parameter
(representing deviation from the symmetric case) in the ¥á−process,
and (3) the occurrence probability of the ¥â−process. In all these
three cases, changes in the type and the degree of population
synchronization are studied in connection with the network topology
such as the degree distribution, the average path length Lp,
and the betweenness centralization Bc.
It is thus found that not only Lp
and Bc
(affecting global communication between nodes) but also the
in-degree distribution (affecting individual dynamics) are important
network factors for effective population synchronization in SFNs.
¡¡
[1] S.-Y. Kim and W. Lim, "Effect of
network architecture on burst and spike synchronization in a
scale-free network of bursting neurons," Neural Networks 79, 53-77
(2016).
¡¡
Thermodynamic and Statistical-Mechanical Measures for Characterization
of Neural Synchronization
¡¡
Synchronized brain rhythms in sleep and awake
states (e.g., alpha, sleep spindle, gamma, ultrafast, beta rhythms), associated
with diverse sensory and cognitive functions, have been observed in electrical
recordings (EEG and local field potentials) of brain activity. Neural
synchronization may be well described by using the population-averaged global
potential VG in computational neuroscience, However, to obtain VG
in real experiments is practically difficult. Instead of VG, the
instantaneous population spike rate (IPSR), which may be obtained
experimentally, is used for description of population behaviors in both
computational and experimental neuroscience. The time-averaged fluctuation of IPSR
plays the role of an order parameter O used for describing the
synchrony-asynchrony transition in neural systems. This order parameter can be
regarded as a thermodynamic measure because it concerns only the macroscopic IPSR
without considering any relation between IPSR and
microscopic individual potentials (spikes). Population spike synchronization may
be well seen in the raster plot of neural spikes. The degree of collective spike
synchronization seen in the raster plot may be well measured in terms of a new
``statistical-mechanical'' spike-based measure Ms introduced by
considering the occupation and the pacing patterns of spikes in the raster plot.
In particular, the pacing degree between spikes is determined in a
statistical-mechanical way by quantifying the average contribution of
(microscopic) individual spikes to the macroscopic IPSR.
This ``statistical-mechanical'' measure Ms is in contrast to the
conventional measures such as the ``thermodynamic'' order parameter (which
concerns the time-averaged fluctuations of the macroscopic global potential),
the ``microscopic'' correlation-based measure (based on the cross-correlation
between the microscopic individual potentials), and the measures of precise
spike timing [based on the peri-stimulus time histogram (PSTH)]. For the
conventional PSTH-based measure ``events,'' corresponding to peaks of the IPSR,
are selected through setting a threshold. Then, the measures for the reliability
and the precision of spike timing concern only the spikes within the events, in
contrast to the case of the ``statistical-mechanical'' measure where all spikes
are considered (without selecting events). A main difference between the
conventional and the new spike-based measures lies in determining the pacing
degree of spikes. The precision of spike timing for the conventional case is
given by just the standard deviation of (microscopic) individual spike times
within an event without considering the quantitative contribution of
(microscopic) individual spikes to the (macroscopic) global activity. Hence, the
PSTH-based measure is not a statistical-mechanical measure. Finally, we
emphasize that both the realistic thermodynamic and statistical-mechanical
measures, based on the IPSR, may be practically applicable for characterization
of neural synchronization in both the computational and the experimental
neuroscience such as spike-timing reliability, stimulus discrimination,
and event related sync./desync.
(1)
Statistical-Mechanical Measure of Stochastic Spiking Coherence in A Population
of Inhibitory Subthreshold Neurons
By
varying the noise intensity, we study stochastic spiking coherence
(i.e., collective coherence between noise-induced neural spikings)
in an inhibitory population of subthreshold neurons (which cannot
fire spontaneously without noise). This stochastic spiking coherence
may be well visualized in the raster plot of neural spikes. For a
coherent case, partially-occupied "stripes" (composed of spikes and
indicating collective coherence) are formed in the raster plot. This
partial occupation occurs due to "stochastic spike skipping" which
is well shown in the multi-peaked interspike interval histogram. The
main purpose of our work is to quantitatively measure the degree of
stochastic spiking coherence seen in the raster plot. We introduce a
new spike-based coherence measure Ms by considering the
occupation pattern and the pacing pattern of spikes in the stripes.
In particular, the pacing degree between spikes is determined in a
statistical-mechanical way by quantifying the average contribution
of (microscopic) individual spikes to the (macroscopic)
ensemble-averaged global potential. This "statistical-mechanical"
measure Ms is in contrast to the conventional measures
such as the "thermodynamic" order parameter (which concerns the
time-averaged fluctuations of the macroscopic global potential), the
"microscopic" correlation-based measure (based on the
cross-correlation between the microscopic individual potentials),
and the measures of precise spike timing (based on the peri-stimulus
time histogram). In terms of Ms, we quantitatively
characterize the stochastic spiking coherence, and find that Ms
reflects the degree of collective spiking coherence seen in the
raster plot very well. Hence, the "statistical-mechanical"
spike-based measure Ms may be used usefully to quantify
the degree of stochastic spiking coherence in a
statistical-mechanical way.
[1] W. Lim and S.-Y.
Kim, "Statisitical-Mechanical Measure of Stochastic Spiking
Coherence in A Population of Inhibitory Subthreshold Neuron", J.
Comput. Neurosci. 31, 667-677 (2011).
[2] S.-Y. Kim and W. Lim, "Realistic thermodynamic
and statistical-mechanical measures for neural synchronization," J. Neurosci.
Methods 226, 161-170 (2014).
(2)
Statistical-Mechanical Measure of Burst and Spike Synchronizations
of Bursting
Neurons
We
are interested in characterization of population synchronization of
bursting neurons which exhibit both the slow bursting and the fast
spiking timescales, in contrast to spiking neurons. Population
synchronization may be well visualized in the raster plot of neural
spikes which can be obtained in experiments. The instantaneous
population firing rate (IPFR), which may be directly obtained from
the raster plot of spikes, is often used as a realistic collective
quantity describing population behaviors in both the computational
and the experimental neuroscience. For the case of spiking neurons,
realistic thermodynamic order parameter and statistical–mechanical
spiking measure, based on IPFR, were introduced in our recent work
to make practical characterization of spike synchronization. Here,
we separate the slow bursting and the fast spiking timescales via
frequency filtering, and extend the thermodynamic order parameter
and the statistical–mechanical measure to the case of bursting
neurons. Consequently, it is shown in explicit examples that both
the order parameters and the statistical–mechanical measures may be
effectively used to characterize the burst and spike
synchronizations of bursting neurons.
[1] S.-Y. Kim and W.
Lim, "Thermodynamic order parameters and statistical-mechanical
measures for characterization of the burst and spike
synchronizations of bursting neurons," Physica A 438, 544-559
(2015).
[2] S.-Y. Kim and W. Lim, "Frequency-domain order parameters for the
burst and spike synchronization transitions of bursting neurons,"
Cognitive Neurodynamics 9, 411-421 (2015).
¡¡
Stochastic Spiking
Coherence in Networks of Subthreshold Neurons
In recent years,
much attention has been paid to brain rhythms. Synchronization of the
firing activity in groups of neurons may be used for efficient sensory
processing (e.g., visual binding). In addition to a constructive role of
encoding sensory stimuli, neural synchronization is also correlated with
pathological rhythms associated with neural diseases (e.g., epileptic
seizures and tremors in Parkinson's disease). Many studies on collective
dynamical behaviors in neural systems were made to understand the
mechanisms of such synchronized firings. However, most of them were
restricted to the suprathreshold case consisting of spontaneously firing
(i.e., self-oscillating) neurons. We note that in addition to
suprathreshold neurons, subthreshold neurons (which can fire only with
the help of noise) also exist in real neural systems. Hence, we must
take into consideration the existence of subthreshold neurons for the
study on the population neurodynamics. For the subthreshold case,
neurons cannot fire spontaneously without noise. Noise is usually
considered as a nuisance, degrading the performance of dynamical
systems. However, in certain circumstances, noise plays a constructive
role in the emergence of dynamical order. A main subject of our study is
to investigate stochastic spiking coherence (i.e., collective coherence
between noise-induced firings) for the subthreshold case. Based on this
study for the subthreshold case, we also study coherent population
dynamics in heterogeneous ensembles composed of subthreshold and
suprathreshold neurons.
(1) Stochastic Spiking
Coherence in Coupled Excitatory Neurons
A.
Characterization of Stochastic Spiking Coherence
We consider a large population of subthreshold Morris-Lecar neurons interacting via global instantaneous
pulse-type excitatory synaptic coupling. By varying the noise intensity, we
investigate numerically stochastic spiking coherence (i.e., collective coherence
between noise-induced neural spikings). As the noise amplitude passes a
threshold, a transition from an incoherent to a coherent state occurs. This
coherent transition is described in terms of the "thermodynamic" order
parameter, which concerns a macroscopic time-averaged fluctuation of the global
potential. We note that such stochastic spiking coherence may be well visualized
in terms of the raster plot of neural spikings (i.e., spatiotemporal plot of
neural spikings), which is directly obtained in experiments. To quantitatively
measure the degree of stochastic spiking coherence (seen in the raster plot), we
introduce a new type of ``spiking coherence measure,'' by taking into
consideration the average contribution of (microscopic) local neural spikings to
the (macroscopic) global membrane potential. Hence, the spiking coherence
measure may be regarded as a "statistical-mechanical" measure. Through
competition between the constructive and the destructive roles of noise,
stochastic spiking coherence is found to occur over a large range of
intermediate noise intensities and to be well characterized in terms of the
mutually complementary quantities of the order parameter and the spiking
measure. Particularly, the spiking measure reflects the degree of stochastic
spiking coherence seen in the raster plot very well.
[1] W. Lim and S.-Y. Kim, "Characterization
of Stochastic Spiking Coherence in Coupled Neurons," J. Korean Phys. Soc. 51,
1427-1431 (2007).
[2] W. Lim and S.-Y. Kim, "Stochastic spiking
coherence in coupled subthreshold Morris-Lecar neurons,"
Int. J. Mod. Phys. B 23, 703-710 (2009).
B. Stochastic
Oscillator Death
We consider an ensemble
of subthreshold Morris-Lecar neurons interacting via global instantaneous
pulse-type excitatory synaptic coupling. As the coupling strength passes a lower
threshold, the coupling stimulates coherence between noise-induced spikings.
This coherent transition is well described in terms of an order parameter.
However, for sufficiently large coupling strength, "stochastic oscillator death"
(i.e., quenching of noise-induced spikings), leading to breakup of collective
spiking coherence, is found to occur. Using the techniques of nonlinear
dynamics, we investigate the dynamical origin of stochastic oscillator death.
Thus, we show that stochastic oscillator death occurs because each local neuron
is attracted to a noisy equilibrium state via an infinite-period bifurcation.
Furthermore, we introduce a new "statistical-mechanical" parameter, called the
average firing probability, and quantitatively characterize a transition from
firing to non-firing states which results from stochastic oscillator death. For
a firing (non-firing) state, the averaging firing probability tends to be
non-zero (zero) in the thermodynamic limit. We note that the role of the average
firing probability for the firing-nonfiring transition is similar to that of the
order parameter used for the coherence-incoherence transition.
[1] W. Lim and S.-Y. Kim, "Stochastic Oscillator
Death in Globally Coupled Neural Systems," J. Korean Phys. Soc. 52, 1913-1917
(2008).
[2] W. Lim and S.-Y. Kim, "Coupling-induced
spiking coherence in coupled subthreshold neurons," Int. J. Mod. Phys. B 23,
2149-2157 (2009).
(2) Stochastic Spiking
Coherence in Coupled Inhibitory Neurons
Depending
on the type of synaptic receptors (e.g., AMPA and GABA), the synaptic coupling
may be excitatory or inhibitory. About 20 % of neurons are inhibitory ones in
the human brain. For example, the principal neurons in the cortex are excitatory
ones, while the interneurons are inhibitory ones. Through the efficient roles of
the inhibitory neurons, the functions of the excitatory neurons are diversified
and their computational abilities are much enhanced. In such a way, the brain
functions may be well performed via balance of excitation and inhibition. Here, we study coherent population dynamics in coupled
inhibitory neurons, and compare them with those in coupled excitatory neurons.
A.
Statistical-Mechanical Measure of Stochastic Spiking Coherence in A
Population of Inhibitory Subthreshold Neurons
By varying the noise intensity, we study stochastic spiking coherence
(i.e., collective coherence between noise-induced neural spikings) in an inhibitory population of subthreshold neurons (which
cannot fire spontaneously without noise). This stochastic spiking coherence may be well visualized in the raster plot of neural
spikes. For a coherent case, partially-occupied "stripes" (composed of spikes and indicating collective coherence) are formed
in the raster plot. This partial occupation occurs due to "stochastic spike skipping" which is well shown in the multi-peaked interspike interval histogram. The main purpose of our work is to quantitatively measure the degree of stochastic spiking coherence
seen in the raster plot. We introduce a new spike-based coherence measure
Ms by considering the occupation pattern and the
pacing pattern of spikes in the stripes. In particular, the pacing degree between spikes is determined in a statistical-mechanical
way by quantifying the average contribution of (microscopic) individual spikes to the (macroscopic) ensemble-averaged global potential.
This "statistical-mechanical" measure
Ms is in contrast to the conventional measures such as the "thermodynamic" order parameter
(which concerns the time-averaged fluctuations of the macroscopic global potential), the "microscopic" correlation-based measure
(based on the cross-correlation between the microscopic individual potentials), and the measures of precise spike timing (based on the
peri-stimulus time histogram). In terms of Ms, we quantitatively characterize the stochastic spiking coherence, and find that
Ms
reflects the degree of collective spiking coherence seen in the raster plot very well. Hence, the "statistical-mechanical" spike-based
measure Ms may be used usefully to quantify the degree of stochastic spiking coherence in a statistical-mechanical way.
[1] W. Lim and S.-Y. Kim, "Statistical-Mechanical Measure of Stochastic Spiking Coherence in A Population of
Inhibitory Subthreshold Neuron", J. Comput. Neurosci. 31, 667-677 (2011).
B. Inhibitory
Coherence in A Heterogeneous Population of Subthreshold and
Suprathreshold Type-I Neurons
We study inhibitory coherence (i.e., collective coherence by synaptic inhibition) in a population of globally coupled type-I neurons which can fire at arbitrarily low frequency. No inhibitory coherence is observed in a homogeneous population composed of only subthreshold neurons which exhibit noise-induced firings. In addition to subthreshold neurons, there exist spontaneously firing suprathreshold neurons in a noisy environment of a real brain. To take into consideration the effect of suprathreshold neurons on inhibitory coherence, we consider a heterogeneous population of subthreshold and suprathreshold neurons, and investigate the inhibitory coherence by increasing the fraction of suprathreshold neurons
Psupra. As
Psupra passes a threshold
Psupra, suprathreshold neurons begin to synchronize and play the role of coherent inhibitors for the emergence of inhibitory coherence. Thus, regularly-oscillating population-averaged global potential appears for
Psupra>
P*supra. For this coherent case suprathreshold neurons exhibit sparse spike synchronization (i.e., individual potentials of suprathreshold neurons consist of coherent sparse spikings and coherent subthreshold small-amplitude hoppings). By virtue of their coherent inhibition, sparsely synchronized suprathreshold neurons suppress noisy activity of subthreshold neurons. Thus, subthreshold neurons exhibit hopping synchronization (i.e., only coherent subthreshold hopping oscillations without spikings appear in the individual potentials of subthreshold neurons). We also characterize the inhibitory coherence in terms of the "statistical-mechanical" spike-based and correlation-based measures which quantify the average contributions of the microscopic individual spikes and individual potentials to the macroscopic global potential. Finally, effect of sparse randomness of synaptic connectivity on the inhibitory coherence is briefly discussed.
[1] S.-Y. Kim, D.-G. Hong, J. Kim, and W. Lim, "Inhibitory coherence in a heterogeneous population of subthreshold and suprathreshold type-I neurons", J. Phys. A 45, 155102 (2012).
C. Effect of
Sparse Random Connectivity on the Stochastic Spiking Coherence of
Inhibitory Subthreshold Neurons
We study the effect of network structure on the stochastic spiking coherence (i.e., collective
coherence between noise-induced neural spikings) in an inhibitory population of subthreshold neurons (which cannot fire spontaneously without noise).
Previously, stochastic spiking coherence was found to occur for the case of global coupling. However, "sparseness" of a real neural network is well known.
Hence, we investigate the effect of sparse random connectivity on the stochastic spiking coherence by varying the average number of synaptic inputs per
neuron Msyn. It is thus found that stochastic spiking coherence emerges if
Msyn is larger than a (very small) critical value
M*syn, independently
of the network size N. This stochastic spiking coherence may be well visualized in the raster plot of neural spikes. For a coherent case, partially-occupied
stripes appear. As Msyn is decreased from
N-1 (globally-coupled case), the average occupation degree of spikes per stripe increases very slowly.
On the other hand, the average pacing degree between spikes per stripe decreases slowly, but near
M*syn its decrease becomes very rapid. This decrease
in the pacing degree can also be well seen through merging of multiple peaks in the interspike interval histograms. Due to the effect of the pacing degree,
the degree of stochastic spiking coherence decreases abruptly near the threshold
M*syn.
[1] D.-G. Hong, S.-Y. Kim, and W. Lim, "Effect of Sparse Random Connectivity on the Stochastic Spiking Coherence of Inhibitory Subthreshold Neurons," J. Korean Phys. Soc. 59, 2840-2846 (2011).
(3) Stochastic Spiking
Coherence in Two Populations of Excitatory and Inhibitory Neurons
Human brain exhibits their
functions well through balance between the excitatory and the
inhibitory neurons. The ratio of inhibitory neurons in the brain is
about 20%. We are interested in collective spiking coherence in two
populations of excitatory and inhibitory neurons. Particularly, we
study the effect of the interpopulation coupling on such spiking coherence. So, by varying the interpopulation coupling strength to keep the E/I balance (i.e., the ratio of AMPA and the GABA conductances is equal for both E- and I-neurons), we investigate coherent population dynamics in each population. Such population dynamics is analyzed using the techniques of the nonlinear dynamics and the statistical mechanics. We also introduce the interpopulation spiking measure between the source and the target populations, and characterize the degree of the interpopulation effect.
A. Interpopulation
Effect on Stochastic Spiking Coherence in Two Populations of
Excitatory and Inhibitory Subthreshold Type-I Neurons
We consider two populations of excitatory and inhibitory subthreshold type-I neurons which can fire at arbitrary low frequency. No coherence occurs in the single inhibitory population, while stochastic excitatory coherence appears in the single excitatory population. Through the coupling between the excitatory source population and the inhibitory target population, coherence may appear in the inhibitory population. By varying the interpopulation coupling strength to keep the E/I balance, we investigate the effect of the interpopulation coupling on the stochastic spiking coherence in each population. The population dynamics in each population is analyzed using the techniques of the nonlinear dynamics and the statistical mechanics. Particularly, we introduce the interpopulation spiking measure between the source and the target population, and characterize the degree of the interpopulation-coupling effect.
Strange Nonchaotic Firing in
the Quasiperiodically-forced Neuron
We
study the transition from a silent state to a spiking state by varying the DC
stimulus in the quasiperiodically-forced neuron. For this
quasiperiodically-forced case, a new type of strange nonchaotic (SN) firing
(spiking or bursting) state is found to appear between the silent state and the
chaotic firing state as an intermediate one. Using a rational approximation to
the quasiperiodic forcing, we investigate the mechanism for the appearance of
such an SN firing state. We thus find that a smooth torus (corresponding to the
silent state) is transformed into an SN firing attractor via a phase-dependent
bifurcation. This is in contrast to the periodically-forced case where the
silent state transforms directly to a chaotic spiking state. These SN firing
states are also found to be be aperiodic complex ones, as in the case of chaotic
spiking states. Hence, aperiodic complex spikings may result from two
dynamically different states with strange geometry (one is chaotic and the other
one is nonchaotic).
[1]
W. Lim and S.-Y. Kim, "Strange nonchaotic bursting in the quasiperiodically forced Hindmarsh-Rose neuron", J. Korean Phys. Soc. 57, 1356~1362 (2010).
[2] W. Lim and S.-Y. Kim "Strange nonchaotic spiking in the quasiperiodically-forced
Hodgkin-Huxley neuron," J. Korean Phys. Soc. 57, 23-29 (2010).
¡¡
Strange Nonchaotic
Response in the Quasiperiodically-forced Neuron
We
study dynamical responses of the self-oscillating neuron under quasiperiodic
stimulation. For the case of periodic stimulation on the self-oscillating
neuron, a transition from a periodic to a chaotic oscillation occurs through
period doublings. We investigate the effect of the quasiperiodic forcing on this
period-doubling route to chaotic oscillation. In contrast to the
periodically-forced case, a new type of strange nonchaotic (SN) oscillating
states (that are geometrically strange but have no positive Lyapunov exponents)
is thus found to appear between the regular and chaotic oscillating states.
Strange fractal geometry of these SN oscillating states, which is characterized
in terms of the phase sensitivity exponent and the distribution of local
finite-time Lyapunov exponent, leads to aperiodic ¡°complex¡± spikings. Diverse
routes to SN oscillations are found, as in the quasiperiodically forced logistic
map.
[1]
W. Lim and S.-Y. Kim, "Strange
nonchaotic oscillations in the quasiperiodically forced Hodgkin-Huxley neuron,"
J. Phys. A 42, 265103 (2009). [PDF]
[2] W. Lim, S.-Y. Kim, and Y. Kim, "Strange nonchaotic responses of the
quasiperiodically forced Morris-Lecar neuron," Prog. Theor. Phys. 121, 671-683
(2009). [PDF]
¡¡
¡¡
¡¡
[BACK]
|
¡¡ |